Here I consider a system of reaction-diffusion equations of the form  ,
,  . The functions
. The functions  are defined on
are defined on 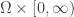 where
where  is a bounded domain in
is a bounded domain in 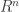 with smooth boundary. Let the
with smooth boundary. Let the 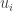 be denoted collectively by
be denoted collectively by  . I assume that the diffusion coefficients
. I assume that the diffusion coefficients 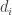 are non-negative. If some of them are zero then the system is degenerate. In particular there is an ODE special case where all
are non-negative. If some of them are zero then the system is degenerate. In particular there is an ODE special case where all 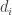 are zero. If this system really describes chemical reactions and the
are zero. If this system really describes chemical reactions and the 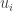 are concentrations then it is natural to assume that
are concentrations then it is natural to assume that  for all
for all  . It should then follow that in the presence of suitable boundary conditions
. It should then follow that in the presence of suitable boundary conditions  for all
for all 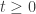 . I assume that
. I assume that  is a classical solution and that it extends to the boundary with enough smoothness that the boundary conditions are defined pointwise. It is necessary to implement the idea that the system is defined by chemical reactions. This can be done by requiring that whenever
is a classical solution and that it extends to the boundary with enough smoothness that the boundary conditions are defined pointwise. It is necessary to implement the idea that the system is defined by chemical reactions. This can be done by requiring that whenever  and
and 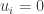 it follows that
it follows that 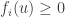 . (This means that if a chemical species is not present it cannot be consumed in any reaction.) It turns out that this condition is enough to ensure positivity.
. (This means that if a chemical species is not present it cannot be consumed in any reaction.) It turns out that this condition is enough to ensure positivity.
I will now explain a proof of positivity. The central ideas are taken from a paper of Maya Mincheva and David Siegel (J. Math. Chem. 42, 1135). Thanks to Maya for helpful comments on this subject. The argument is already interesting for ODE since important conceptual elements can already be seen. I will first discuss that case. Consider a solution of the equation  on the interval
on the interval 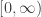 where
where  and
and  are continuous functions with
are continuous functions with  and suppose that
and suppose that  . I claim that
. I claim that  for all
for all 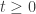 . Let
. Let ![t^*=\sup\{t_1:u(t)\ge 0\ {\rm on}\ [0,t_1]\}](https://s0.wp.com/latex.php?latex=t%5E%2A%3D%5Csup%5C%7Bt_1%3Au%28t%29%5Cge+0%5C+%7B%5Crm+on%7D%5C+%5B0%2Ct_1%5D%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) . Since
. Since  it follows by continuity that
it follows by continuity that  . Assume that
. Assume that  . By continuity
. By continuity  . If
. If 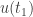 were greater than zero then by continuity it would also be positive for
were greater than zero then by continuity it would also be positive for  slightly larger than
slightly larger than 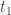 , contradicting the definition of
, contradicting the definition of 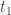 . Thus
. Thus  . The evolution equation then implies that
. The evolution equation then implies that  . This implies that
. This implies that  for
for  slightly less than
slightly less than 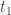 , which also contradicts the definition of
, which also contradicts the definition of 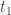 . Hence in reality
. Hence in reality 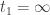 and this completes the proof of the desired result.
and this completes the proof of the desired result.
Suppose now that we weaken the assumptions to  and
and  . We would like to conclude that
. We would like to conclude that  for all
for all  . To do this we define a new quantity
. To do this we define a new quantity  for positive constants
for positive constants  and
and  . Then
. Then 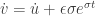 . Hence
. Hence ![\dot v=-au+[b+\epsilon\sigma e^{\sigma t}]](https://s0.wp.com/latex.php?latex=%5Cdot+v%3D-au%2B%5Bb%2B%5Cepsilon%5Csigma+e%5E%7B%5Csigma+t%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) and
and  . Now
. Now  and so
and so ![\dot v=-av+[b+\epsilon(\sigma+a) e^{\sigma t}]](https://s0.wp.com/latex.php?latex=%5Cdot+v%3D-av%2B%5Bb%2B%5Cepsilon%28%5Csigma%2Ba%29+e%5E%7B%5Csigma+t%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) . It follows that if
. It follows that if  is large enough
is large enough  satisfies the conditions satisfied by
satisfies the conditions satisfied by  in the previous argument and it can be concluded that
in the previous argument and it can be concluded that  for all
for all  . Letting
. Letting  tend to zero shows that
tend to zero shows that  for all
for all  , the desired result.
, the desired result.
This is different, and perhaps a bit more complicated than, the proof I know for this type of result. That proof involves considering the derivative of  on
on  . It also involves approximating non-negative data by positive data. A difference is that the proof just given does not use the continuous dependence of solutions of an ODE on initial data and in that sense it is more elementary. In Theorem 3 of the paper of Mincheva and Siegel the former proof is extended to a case involving a system of PDE.
. It also involves approximating non-negative data by positive data. A difference is that the proof just given does not use the continuous dependence of solutions of an ODE on initial data and in that sense it is more elementary. In Theorem 3 of the paper of Mincheva and Siegel the former proof is extended to a case involving a system of PDE.
Now I come to that PDE proof. The system of PDE concerned is the one introduced above. Actually the paper requires the 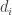 be positive but that stronger condition is not necessary. This equation is solved with an initial datum
be positive but that stronger condition is not necessary. This equation is solved with an initial datum  and a boundary condition
and a boundary condition 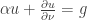 . Here
. Here  is a diagonal matrix with non-negative entries and the function
is a diagonal matrix with non-negative entries and the function  is non-negative. The derivative
is non-negative. The derivative 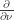 is that in the direction of the outward unit normal to the boundary. We assume that
is that in the direction of the outward unit normal to the boundary. We assume that  is a classical solution, i.e. all derivatives of
is a classical solution, i.e. all derivatives of  appearing in the equation exist and are continuous. Moreover
appearing in the equation exist and are continuous. Moreover  has a continuous extension to
has a continuous extension to 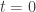 and a
and a 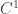 extension to
extension to  . We now replace the differential equation by the differential inequality
. We now replace the differential equation by the differential inequality  . We assume that the initial data are non-negative,
. We assume that the initial data are non-negative, 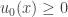 . The assumption that
. The assumption that  is non-negative, together with the boundary condition, gives rise to the inequality
is non-negative, together with the boundary condition, gives rise to the inequality  . The aim is to show that all solutions of the resulting system of inequalities are non-negative. We assume the condition for a system of chemical reactions already mentioned.
. The aim is to show that all solutions of the resulting system of inequalities are non-negative. We assume the condition for a system of chemical reactions already mentioned.
The proof is a generalization of that already given in the ODE case. The first step is to treat the case where each of the inequalities is replaced by the corresponding strict inequality. In contrast to the proof in the paper we assume that that 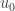 is strictly positive on
is strictly positive on  . We define
. We define 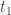 as in the ODE case so that
as in the ODE case so that ![[0,t_1]](https://s0.wp.com/latex.php?latex=%5B0%2Ct_1%5D&bg=ffffff&fg=333333&s=0&c=20201002) is the longest interval where the solution is non-negative. We suppose that
is the longest interval where the solution is non-negative. We suppose that 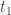 is finite and obtain a contradiction. Note first that, as in the ODE case,
is finite and obtain a contradiction. Note first that, as in the ODE case,  by continuity. Now
by continuity. Now  . If
. If 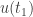 were strictly positive on
were strictly positive on  then by continuity
then by continuity  would be strictly positive for
would be strictly positive for  slightly greater than
slightly greater than 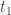 , contradicting the definition of
, contradicting the definition of 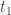 . Hence there is an index
. Hence there is an index  and a point
and a point  with
with 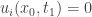 and
and 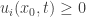 for all
for all 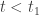 . Suppose first that
. Suppose first that  . Then
. Then  and
and  . This contradicts the strict inequality related to the evolution equation for
. This contradicts the strict inequality related to the evolution equation for 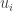 and so cannot happen. Suppose next that
and so cannot happen. Suppose next that 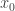 is on the boundary of
is on the boundary of  . Then
. Then 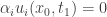 and
and  . This contradicts the strict inequality related to the boundary condition for
. This contradicts the strict inequality related to the boundary condition for 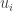 . Thus in fact
. Thus in fact 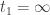 and
and  is strictly positive for all time.
is strictly positive for all time.
Now we do a perturbation argument by considering 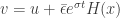 . Here
. Here 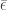 is the vector all of whose components are
is the vector all of whose components are  and
and  is a positive function. It is obvious that
is a positive function. It is obvious that 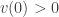 . We now choose
. We now choose  which ensures its positivity and require that the outward normal derivative of
which ensures its positivity and require that the outward normal derivative of 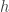 on the boundary is equal to one. (Here I will take for granted that a function
on the boundary is equal to one. (Here I will take for granted that a function 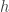 of this kind exists. A source for this statement is cited in the paper. For me the positivity statement is already very interesting in the case that
of this kind exists. A source for this statement is cited in the paper. For me the positivity statement is already very interesting in the case that  is a ball and there the existence of the function
is a ball and there the existence of the function 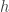 is obvious.) Then the fact that
is obvious.) Then the fact that  satisfies the non-strict boundary inequality implies that
satisfies the non-strict boundary inequality implies that  satisfies the strict boundary inequality. It remains to derive an evolution equation for
satisfies the strict boundary inequality. It remains to derive an evolution equation for  . A straightfoward calculation gives
. A straightfoward calculation gives ![\frac{\partial v_i}{\partial t}-d_i\Delta v_i-f_i(v)\ge e^{\sigma t}\epsilon[\sigma H-d_i\Delta H-L\sqrt{n}H]](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%5Cpartial+v_i%7D%7B%5Cpartial+t%7D-d_i%5CDelta+v_i-f_i%28v%29%5Cge+e%5E%7B%5Csigma+t%7D%5Cepsilon%5B%5Csigma+H-d_i%5CDelta+H-L%5Csqrt%7Bn%7DH%5D&bg=ffffff&fg=333333&s=0&c=20201002) where
where  is a Lipschitz constant for
is a Lipschitz constant for  on the image of the compact region being considered. Choosing
on the image of the compact region being considered. Choosing  large enough ensures that the right hand side and hence the left hand side of this inequality is strictly positive. We conclude that
large enough ensures that the right hand side and hence the left hand side of this inequality is strictly positive. We conclude that  and, letting
and, letting  , that
, that  .
.
If we want to prove an inequality for solutions of a PDE it is common to proceed as follows. We deform the problem continuously as a function of a small parameter  so as to get a simpler problem. When that has been solved we let
so as to get a simpler problem. When that has been solved we let  tend to zero to get a solution of the original problem. Often it is the equations which are deformed. Then we need a theorem on existence and continuous dependence to get a continuous deformation of the solution. The above proof is different. We perturb the solution in a way whose continuity is obvious and then derive a family of equations of which that is a family of solutions. This is easy and comfortable. The hard thing is to guess a good deformation of the soluion.
tend to zero to get a solution of the original problem. Often it is the equations which are deformed. Then we need a theorem on existence and continuous dependence to get a continuous deformation of the solution. The above proof is different. We perturb the solution in a way whose continuity is obvious and then derive a family of equations of which that is a family of solutions. This is easy and comfortable. The hard thing is to guess a good deformation of the soluion.
. I consider the situation where for structural reasons
is always a steady state. Hence
for a smooth function
. The equation
could potentially have a bifurcation at the origin but here I specifically consider the case where it does not. The assumptions are
and
. Moreover it is assumed that
. By the implicit function theorem the zero set of
is a function of
. By the last assumption made the derivative of this function at zero is non-zero. The graph crosses both axes transversally at the origin. It will be supposed, motivated by intended applications, that
. If
there exist positive steady states for
and if
there exist positive steady states with
. The conditions which have been required of
can be translated to conditions on
. Of course
and
. Since
we also have
and the origin is a bifurcation point for
. The other two conditions on
translate to
and
. It follows from the implicit function theorem, applied to
that the bifurcation can be reduced by a coordinate transformation to the standard form
. Thus we see how many steady states there are for each value of
and what their stability properties are.
and
for the bifurcation are defined. They are expressed in invariant form both in terms of the extrinsic dynamical system and in a form intrinsic to the centre manifold. In the coordinate form used above
and
. Theorem 4 of the paper makes statements about the existence and stability of positive steady states which are essentially equivalent to those made above when it is taken into account that in the situation of the theorem the centre manifold is asymptotically stable with respect to perturbations in the transverse directions. It does not say more than that. The fact, often seen in pictures of backward bifurcation that the unstable branch undergoes a fold bifurcation is not included. In particular the fact that for some parameter values there exists more than one positive steady state is not included.