One-dimensional centre manifolds

I have used one-dimensional centre manifolds in my research on several occasions. I now see that I always did this in quite an ad hoc way. I did not exercise due diligence in the sense that I did not take the time to get a general picture of what was going on, so as to be able to use this technique more efficiently in the future. Now I want to do so. I start with the two ODE $\dot x=f(x,y)$ and $\dot y=-y+g(x,y)$ . This example is general enough to illustrate several important ideas. Here $f$ and $g$ are supposed to be smooth and vanish at least quadratically near the origin. The linearization of this system has the eigenvalues $-1$ and zero. Its kernel is spanned by the vector with components $(1,0)$ . It follows that there exists a centre manifold of the form $y=\psi (x)$ , where $\psi$ has any desired finite degree of differentiability. By definition this manifold is invariant under the flow of the system, it passes through the origin and its tangent space there is the $x$ axis. Consider the Taylor expansion $f(x,y)=a_{2,0}x^2+a_{1,1}xy+a_{0,2}y^2+a_{3,0}x^3+\ldots$ . Substituting this into the evolution equation for $x$ gives $\dot x=a_{2,0}x^2+\ldots$ . This is a leading order approximation to the flow on the centre manifold. If $a_{2,0}\ne 0$ we can use it to read off the stability of the origin within the centre manifold. This argument uses no information about the way the centre manifold deviates from the centre subspace, i.e. how fast $\psi$ grows near zero. If $a_{2,0}=0$ we need to go further.

Differentiating the defining equation with respect to time and substituting the evolution equations into the result gives $\psi'(x)f(x,\psi(x))=-\psi(x)+g(x,\psi(x))$ . Call this equation (*). It can be analysed with the help of the Taylor expansions $g(x,y)=b_{2,0}x^2+b_{1,1}xy+b_{0,2}y^2+b_{3,0}x^3+\ldots$ and $\psi(x)=c_2x^2+\ldots$ . Substituting these into (*) we see that the left hand side is of order three. Thus the same must be true of the right hand side and we get $\psi(x)=g(x,\psi(x))+\ldots$ and $c_2=b_{2,0}$ . Substituting this back into the evolution equation for $x$ gives $\dot x=a_{2,0}x^2+(a_{1,1}b_{2,0}+a_{3,0})x^3+\ldots$ . Thus if $a_{2,0}=0$ the stability of the origin is determined by the sign of $a_{1,1}b_{2,0}+a_{3,0}$ . If it is zero we can do another loop of the same kind. Looking at the third order terms in the equation (*) we get $c_3=(-2a_{2,0}+b_{1,1})b_{2,0}+b_{3,0}$ . This allows the fourth order term in the evolution equation for $x$ to be determined. This procedure can be repeated as often as desired to get higher order approximations for the centre manifold and the restriction of the system to that manifold.

We can now sum up the steps involved in doing a stability analysis. First look at the coefficient of $x^2$ in the equation for $\dot x$ . If it is non-zero we are done. If it is zero use the equation (*) to determine the leading term in the expansion of the centre manifold. Put this information into the equation for $\dot x$ . If the leading term is non-zero we are done. If it is zero we can repeat the process as long as is necessary to get a case in which the leading order coefficient is non-zero. As long as this point has not been reached we cycle between using (*) and the equation for $\dot x$ . The system I have discussed here was special. The codimension of the centre manifold was one and the system was in a form which usually could only be achieved by a preliminary linear transformation of the coordinates. The special case nevertheless exhibits the essential structure of the general case and can serve as a compass when treating examples.

These ideas can be extended to give information about bifurcations. The equations are replaced by $\dot x=f(x,y,\alpha)$ and $\dot y=-y+g(x,y,\alpha)$ , where $\alpha$ is a parameter. This can be made into a three-dimensional extended system by adding the equation $\dot\alpha=0$ . The origin is a steady state of the extended system and the centre manifold at that point is of dimension two. It is of the form $y=\psi (x,\alpha)$ . Suppose that we are in the case $a_{2,0}\ne 0$ . Then this looks very much like the case of a generic fold bifurcation. We are just missing one condition on the parameter dependence. The dynamics on the centre manifold is given by $\dot x=f(x,\psi(x,\alpha),\alpha)=h(x,\alpha)$ . Of course the equation $\dot \alpha=0$ remains unchanged. We can now check the conditions for a generic fold bifurcation in the system reduced to the centre manifold. The first is $h(0,0)=f(0,0,0)=0$ . The second is $h_x(0,0)=f_x(0,0,0)+\psi_x(0,0)f_y(0,0,0)$ . Hence $h_x(0,0)=0$ is equivalent to $f_x(0,0,0)=0$ . The third involves $h_{xx}(0,0)=f_{xx}(0,0,0)+\psi_{xx}(0,0)f_y(0,0,0)+2\psi_x(0,0)f_{xy}(0,0,0)+\psi_x^2(0,0)f_{yy}(0,0,0)$ . We see that $h_{xx}(0,0)\ne 0$ is equivalent to $f_{xx}(0,0,0)\ne 0$ . The fourth involves $h_\alpha (0,0)=\psi_\alpha(0,0)f_y(0,0,0)+f_\alpha(0,0,0)$ . We see that $h_\alpha (0,0)\ne 0$ is equivalent to $f_\alpha(0,0,0)\ne 0$ . The first three conditions for a generic fold bifurcation of the system on the centre manifold are already satisfied and the fourth is equivalent to $f_\alpha(0,0,0)\ne 0$ . In this way the bifurcation conditions can be expressed directly in terms of the coefficients of the original system. This is an illustration in a relatively simple example of a relationship discussed in much more general cases in the book of Kuznetsov.

This entry was posted on March 18, 2024 at 4:56 pm and is filed under analysis, dynamical systems. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

2 Responses to “One-dimensional centre manifolds”

hydrobates Says:
April 11, 2024 at 11:41 am | Reply
When this was originally posted some important terms were omitted. This problem has now been corrected.
hydrobates Says:
April 18, 2024 at 7:20 am | Reply
The above discussion can be made more concrete with the help of a good example, such as Example 5.1 in Kuznetsov’s book. In that case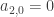 $a_{2,0}=0$ , $a_{1,1}b_{2,0}+a_{3,0}=-1$ and the steady state is stable. A phase portrait in the book shows what is going on.

Hydrobates